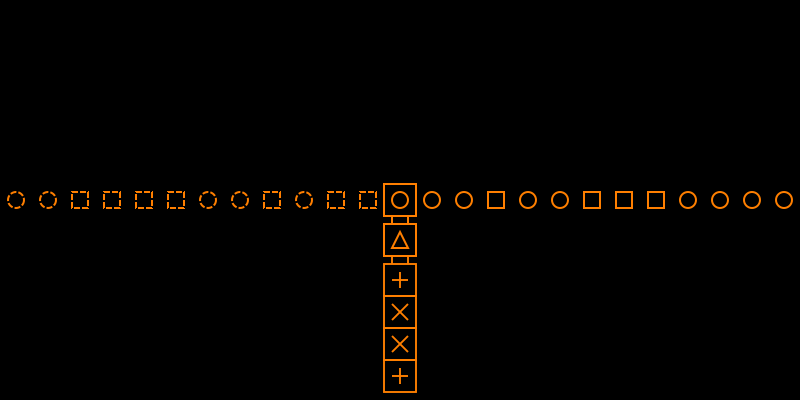
上下文无关文法，以及下推自动机——形式语言和自动机的那一套理论【2】

没错，这是第二部分。 以下就进入正题了。

上下文无关文法

正则表达式能够表示的语言都比较简单，上下文无关文法则可以表示更加复杂的语言。

一个上下文无关文法包括：一个字符集、一个变元集合以及一个产生式集合，并且变元集合中有一个变元被称为初始变元。所谓产生式就是 S→aSb 这样的，由一个变元变成变元和字符组成的串的式子。为了方便，我们会把左侧变元相同的产生式合并，比如 S→SS|(S)|ε。

我们这样得到一个上下文无关文法对应的语言：我们从一个单个初始变元组成的串开始，每次选择一个串中的变元，将其按照某个产生式替换成一个变元变成变元和字符组成的串。这样的替换过程称为一次推导。不断进行推导，直到串中只有字符没有变元，所有可以这样得到的串组成的集合称为上下文无关文法对应的语言，这样的语言称为上下文无关语言。

事实上，文法中的每个变元都对应一个语言。

在推导时我们可以选择只替换最左侧或最右侧的变元，这样整个推导过程就可以称为最左推导或最右推导。推导过程中得到的串称为句型。

如果我们把推导的过程用给节点添加子节点的过程表示，我们就得到了语法分析树。如下图是一个语法分析树的例子：

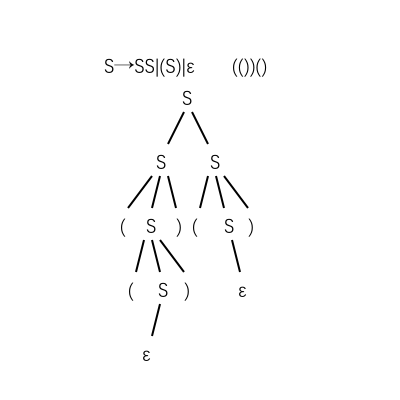
从语法分析树也可以容易地构造推导过程，只需要中序遍历一下树就好了。

如果一个上下文无关文法对应的语言中有一个串有多个不同的语法分析树，那么这个文法就称为有歧义的。而如果一个上下文无关语言对应的文法一定是有歧义的，那么这个语言就称为固有歧义的。

事实上有一个串多个不同的语法分析树当且仅当这个串有多个不同的最左推导，同时当且仅当有多个不同的最右推导。

很多文法可以经过修改去除歧义性，但是有固歧义的语言对应的文法不行。 上下文无关文法经常用来描述各种编程语言、标记语言等的语法。

下推自动机

下推自动机可以理解为一个有限自动机加上一个栈。

下推自动机有一个状态和一个栈。状态只有有限种，而栈里可以存放任意个一个有限字符集中的字符。下推自动机有一个初始状态、并且初始时栈里有一个初始字符。每当下推自动机接受一个字符，或是自发地进行一次状态转换，我们可以根据现在的栈顶字符和状态以及输入的字符，选择新的状态，并从栈中取出栈顶字符然后压入一堆字符。如果栈中没有字符了，下推自动机就不接受新字符了。

下推自动机可以用下面这样的图来表示：

有两种判断下推自动机是否接受一个串的方式，一种是看最终自动机的状态（以终结方式接受），另一种是看自动机最终是否已经清空（以空栈方式接受）。

一个语言是某个以终结方式接受的下推自动机对应的语言当且仅当它是某个以空栈方式接受的下推自动机对应的语言，这样以哪一种方式接受语言就显得不那么重要。

事实上，对于以终结方式接受的下推自动机，我们可以构造对应的以空栈方式接受的下推自动机。只需要使用新栈内初始字符，在原来的初始状态前增加一个状态，并且可以从这个新状态自动进入原来的初始状态并同时在栈内添加原来的栈内初始字符，然后从原来的终结状态可以自动进入另一个新状态，而在这个新状态内可以自动清空整个栈即可。这样原下推自动机以终结方式接受的串就会被新下推自动机以空栈方式接受，而其他的串不会被以空栈方式接受。特别的，原下推自动机不以终结方式接受的但是会清空栈的串，在新下推自动机中只会让栈中余下一个新的栈内初始字符。

反过来，对于以空栈方式接受的下推自动机，我们可以构造对应的以终结方式接受的下推自动机。只需要使用新栈内初始字符，在原来的初始状态前增加一个状态，并且可以从这个新状态自动进入原来的初始状态并同时在栈内添加原来的栈内初始字符，然后从原来的状态可以拿出新的栈内初始字符并进入另一个新的终结状态。这样原下推自动机以空栈方式接受的串就会被新下推自动机以终结方式接受，而其他的串不会被以空栈方式接受。事实上，一个串能被原下推自动机以空栈方式接受当且仅当这个串会让新下推自动机的栈中余下一个新的栈内初始字符，并随后进入终结状态。

一个不平凡的事实是，如果一个语言是上下文无关语言，也即有对应的上下文无关文法，那么它有对应的下推自动机。 事实上，我们可以这样构造文法对应的以空栈方式接受的下推自动机：我们的自动机只有一个状态，合法的栈内字符可以是文法中的所有字符和变元。初始时的栈内字符是文法的初始变元，而下推自动机可以自动地从栈中拿出一个变元并以逆序压入其对应的产生式右侧的串，或者接受一个字符并从栈中拿出对应的该字符。我们可以看出，此时下推自动机的运作方式等同于最左推导，因而结论成立。

另一个不那么平凡的结论是，如果一个语言有对应的下推自动机，那么它是上下文无关语言，也即有对应的上下文无关文法。

事实上，我们可以这样构造以空栈方式接受的下推自动机对应的文法：对于任意两个状态 p,q 和一个栈内字符 X，我们定义变元 [pXq]，它对应的是能使自动机从 p 状态转移到 q 状态，并从栈内恰好取出 X 的串的集合。令 S 为初始变元。对于初始状态 p_0，栈内初始字符 Z 和任意状态 p，有 S→[p_0Zp]。而若下推自动机可以接受字符 a（或者是 ε 如果是自动的状态变化）从状态 p 转换到 q，并从栈中取出 X 并压入 Y_1Y_2…Y_k，那么对于任意状态 p_1,p_2…p_k，有 [pXp_k]→a[qY_1p_1][p_1Y_2p_2]…[p_{k-1}Y_kp_k]。特别的，k=0 时有 [pXq]→a 。这样我们就得到了对应的文法，很容易归纳证明其正确性。

这样我们就有，一个语言有对应的下推自动机当且仅当它是上下文无关语言，也即有对应的上下文无关文法。

确定型下推自动机

如果下推自动机对于任何一个状态和栈顶字符的组合都只能自动转移至一个确定的新状态并确定地改变栈，或者接受一个字符并根据此字符转移至一个确定的新状态并确定地改变栈，那么这个下推自动机称为确定型下推自动机。 和有限自动机的情况不同的是，并非所有上下文无关语言都有对应的确定型下推自动机。甚至，以空栈方式接受的确定型下推自动机对应的语言类和以终结方式接受的确定型下推自动机对应的语言类是不同的。

以空栈方式接受的确定型下推自动机所接受的语言中不能有一个串是另一个串的前缀，事实上，由于确定型下推自动机的栈不能变空两次，这个结论是显然的。这导致甚至很多正则语言，没有对应的以空栈方式接受的确定型下推自动机。

以空栈方式接受的确定型下推自动机对应的语言一定有对应的以终结方式接受的确定型下推自动机。事实上，直接使用对于一般的下推自动机的构造就可以了。

另一方面，以终结方式接受的确定型下推自动机对应的语言只要满足其中没有一个串是另一个其中的串的前缀，就有对应的以空栈方式接受的确定型下推自动机。事实上，直接使用对于一般的下推自动机的构造，然后把原来的终结状态对应的转移全删掉就可以了。

于是，一个语言有以对应的空栈方式接受的确定型下推自动机当且仅当它有对应的以终结方式接受的确定型下推自动机并且其中没有一个串是另一个其中的串的前缀。

当然，以终结方式接受的确定型下推自动机可以直接模拟有限自动机，于是以终结方式接受的确定型下推自动机对应的语言类在正则语言和上下文无关语言之间。

另一方面，以空栈方式接受的确定型下推自动机对应的语言必然有无歧义文法。事实上，直接使用对于一般的下推自动机的构造即可。文法的无歧义性可以由下推自动机是确定的推得。而对于以终结方式接受的确定型下推自动机这个结论也成立。事实上，我们在原语言后面加上一个新字符，那么新语言当中没有一个串是另一个其中的串的前缀，于是就有对应的以空栈方式接受的确定型下推自动机从而无歧义，然后我们再把新字符变成变元，并且它只能推出空串，那么我们就能得出结论成立。

一些性质、结论、以及问题和解决方案 我们可以对文法进行一些等价变换，使得它满足一些性质。

首先我们可以去除推导中不可能用到的变元和字符，以及对应语言为空的变元。通过引用关系的有向图我们可以轻松的做到这一点。 其次我们可以仅仅以从语言中去除空串为代价，让文法中产生式右侧没有空串。我们可以递归地找到可以为空的变元，并将出现过它们的产生式改写为多个等价的产生式。

然后我们还可以去除像 A→B 这样的由一个变元推导到另一个变元的单位产生式。我们可以递归地找到所有的单位变元对，并增加它们的产生式来代替单位产生式。

最后，我们可以把所有产生式都变为 A→BC （A,B,C 为变元）或 A→a （A 为变元，a 为字符）的形式。首先我们进行上面的三种操作，其后我们对每个字符都构造第二种形式的产生式，并将有多余三个变元的产生式改写为第一种形式即可。

这样我们就构造出了（几乎）等价且符合乔姆斯基范式的文法。这时语言对应的语法分析树一定是二叉树。

需要注意的是，如果我们提前减小产生式的长度，产生乔姆斯基范式的速度会显著提高。

与正则语言类似，上下文无关语言也有泵引理。由于语言中串足够长的时候（大于最长产生式长度的变元数量次方）时，语法分析树的高度就会高于变元数量，那么必然有一个树上从根到叶的路径上有同一个变元出现了两次，于是考虑这两个相同的变元将语法分析树分隔成的各部分，便有：对任意的上下文无关语言，都存在常数 n，使得对其中的串 z，只要 z 的长度大于 n，就存在串 u,v,w,x,y 使得 z=uvwxy，vx不为空串，vwx 的长度不大于 n，以及对于任意的自然数 k，uvvv…vwxxx…xy（中间有 k 个 v 和 k 个 x）都属于这个语言。这个引理可以用来证明一些语言不是上下文无关语言。

上下文无关语言在如下的代入运算后还是上下文无关语言：将每一个字符都替换成对应的另一个上下文无关语言中的任意串。我们只需把原语言的产生式中的字符全部换成变元，并合并诸语言的文法即可。由此可以推出，上下文无关语言的并、连接、闭包、同态都是上下文无关语言。

上下文无关语言的反转也是上下文无关语言，只需把文法中的产生式也反转即可。

然而，上下文无关语言的交不一定是上下文无关语言。

正则语言与上下文无关语言的交是上下文无关语言，我们只需用下推自动机的状态模拟上下文无关语言的下推自动机的状态和正则语言的有限状态机的状态，用它的栈模拟上下文无关语言的下推自动机的栈即可。

上下文无关语言的逆同态也是上下文无关语言。我们用下推自动机模拟原语言的下推自动机的多步运行即可。需要注意的是，我们不能一步从栈里弹出多个字符，但是利用自动转移和额外状态我们还是可以做到这一点。

通过去除推导中不可能用到的变元和字符以及对应语言为空的变元的过程，我们可以判断文法对应的语言是否为空。

利用乔姆斯基范式以及动态规划我们可以测试一个串是否属于一个上下文无关语言。我们只需从短到长测试串的各个字串属于哪些变元的语言即可。

判断上下文无关文法是否有歧义，上下文无关语言是否有歧义，两个上下文无关语言交是否为空，两个上下文无关语言是否等价，某个上下文无关语言是否包含所有可能的串都是不可判定的。

结尾

以上就是上下文无关文法以及下推自动机相关的笔记。能读下来真是太感谢了……

下周就要考试了，在那之前作为复习来把第三部分写出来吧。

下一个笔记会是图灵机、问题类等等相关的内容，有兴趣的话欢迎来看。