确定和不确定的有限自动机，以及正则表达式——形式语言和自动机的那一套理论【1】

这学期有一门课叫做形式语言与自动机。尽管这门课主要是为下个学期编译原理打基础的，但是也附带了一些计算理论的东西。 因为再过几周就要期末考试了，加之这课内容还是蛮好玩的，所以就来写一点笔记大致过一下。

这里的大部分内容来自于课本，但是也有一些之外的东西。

我在这里不会采取特别形式化的描述，毕竟不是正经的学术文章。另一方面，这是写给自己看的笔记，所以读不下去也很正常。

以下就进入正题了。

语言

我们先来定义什么叫一门语言。

所谓语言，就是字符串的集合。当然，字符串中的字母只能有有限种，字符串只能有有限长。

语言既然是集合，那么语言之间就可以交并补运算。除此之外，因为字符串可以连接、反转等等，语言也有连接、反转等运算。

我们还定义闭包运算：由一个语言中的若干个（0 个也可以）字符串顺序连接起来得到的字符串组成的语言称为语言的闭包。

还有同态运算：把串中每一个字母替换成对应的串得到新语言的运算成为同态运算。反过来的过程称为逆同态

自动机

我们再来定义什么是自动机。

自动机就是一个有内部状态的机器。它有一个初始状态，而每当它接收到一个字符，它就根据字符和当前的内部状态，更新自己的内部状态（新状态与旧状态和输入字符之间的函数关系称为状态转移函数），而当所有字符都处理完之后，我们根据自动机的最终状态，将接受的字符串分为两类：自动机接受的字符串和自动机不接受的字符串。

自动机接受的字符串集合当然也是语言，这称为自动机对应的语言。

我们也可以允许自动机有多个可能的状态，这种情况下我们把多个可能的状态组成的集合作为自动机的内部状态，这样的自动机就是非确定型的自动机。

这样我们也可以允许自动机的状态在不接受字符的时候自动转移，只需要把自动转移后的状态也列入可能的状态集合，这样的自动机就是带 ε-转移的非确定型的自动机。

有限自动机

如果自动机只有有限种可能的状态，那自动机就是有限状态机。

如果有限状态机无论处理了什么串之后都总是只有一种可能的状态，那就是确定型的有限状态机，不然就是非确定型的有限状态机。

我们规定，有限状态机接受某个字符串当且仅当最终可能的状态包含某些状态中的一个。

有限状态机可以用下面这样的图来表示：

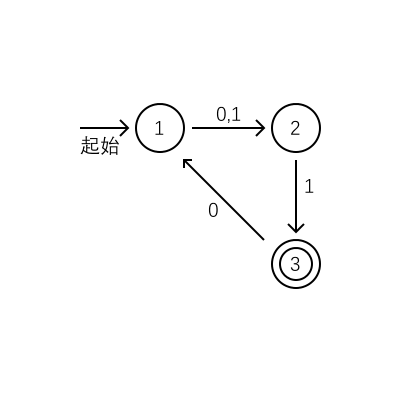
显然确定型的有限状态机对应的语言都有对应的非确定型的有限状态机，而由于状态集合的子集也只有有限种，于是反过来也是成立的。当然，在从非确定型的有限状态机构造确定型的有限状态机时，我们只需要考虑那些可能出现的状态集。

有限自动机可以在文本搜索之类的地方运用。

正则表达式

我们用字符表示一个单字符的串构成的语言，用ε表示空串，用∅表示空语言，然后对它们进行连接（直接连接）、或（+）、闭包（*）操作，可以得到新语言。我们用正则表达式表示这样的新语言，比如 10*0+(101*0)* 之类的。

注意，这里的正则表达式和各编程语言和库中的正则表达式相比能力要弱一些。

一个不那么平凡的结论是，正则表达式可以表示任何一个有限状态机对应的语言。

一种构造有限状态机对应的正则表达式的方式是这样的：给所有的状态编一个编号，然后归纳地构造能让自动机从状态 i 转移到状态 j 且中途只经过前 k 种状态的字符串构成的语言的正则表达式 R[i][j][k]。R[i][j][0] 是容易构造的，而 R[i][j][k]=R[i][j][k-1]+R[i][k][k-1]R[k][k][k-1]*R[k][j][k]，于是我们对于任何两个状态都有了能使自动机从第一个状态转移到第二个状态的字符串组成的语言对应的正则表达式，然后对照初始状态和可接受的终结状态，将对应的正则表达式或一下，我们就得到了确定型的有限状态机对应的正则表达式。

另一种构造方式是这样的：我们把有限状态机从接受字符推广为接受正则表达式，对应的语言则是可接受的正则表达式串的并对应的语言。首先我们可以假定可接受的终结状态只有一种。我们定义从状态 i 到 状态 j 所接受的正则表达式是 R[i][j]。我们不断地消除既非初始状态也非终结状态的状态 s，并对于任意其他状态 i,j，我们把 R[i][j] 改写为 R[i][j]+R[i][s]R[s][s]*R[s][j]，直到只剩下初始状态 b 和终结状态 e。这时，若 b=e，对应的正则表达式就是 R[b][b]*，若 b!=e， 则对应的正则表达式是 R[b][b]*R[b]e*。

另一个不那么平凡的结论是，任何一个正则表达式表示的语言都有对应的有限状态机。

事实上，如下图构造就好了：

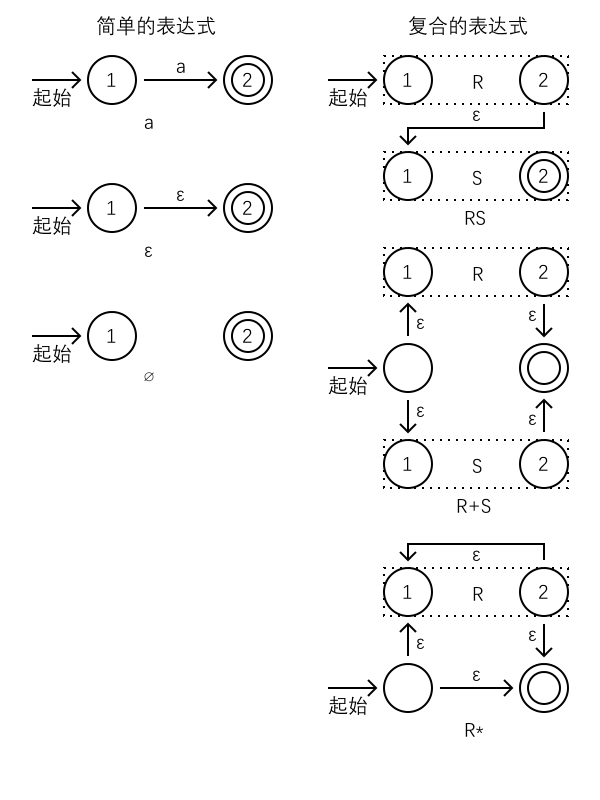
于是一个语言能被正则表达式表示当且仅当它有对应的有限状态机，这样的语言称之为正则语言。

一些性质、结论、以及问题和解决方案

如果我们考虑状态集合为两个有限状态机的状态集合的笛卡尔乘积的有限状态机，我们就可以得知两个正则语言的交并补也都是正则语言。

因为正则表达式有连接和闭包操作，所以正则语言的连接和闭包也都是正则语言。

由于你可以把正则表达式中的字符都替换成字符串，所以正则语言在同态变换后也是正则语言。

由于你可以把任何的字符输入转换成对应的字符串输入，所以正则语言在逆同态变换后也是正则语言。

只需要考虑以有限状态机的状态为顶点的有向图的连通性，便可以判断有限状态机对应的语言是否为空。直接简单模拟一下有限状态机便可以知道一个串是否属于有限状态机对应的语言。

由于有限状态机的状态只有有限种，于是只要一个串长度足够长，有限状态机处理这个串的时候就必然会两次进入同一个状态。于是就有这个定理：对任意的正则语言，都存在常数 n（可以取有限状态机的状态数量），使得对其中的串 w，只要 w 的长度大于 n，就存在串 x,y,z 使得 w=xyz，y不为空串，xy 的长度不大于 n，以及对于任意的自然数 k，xyyyy…yz（中间有 k 个 y）都属于这个语言。这称为正则语言的泵引理。这个引理可以用来证明一些语言不是正则语言。

我们再来考虑确定型的有限状态机的等价状态问题。两个串被认为是等价的当且仅当对于任意串，分别以这两个状态为起始状态处理完这个串之后要么都处于接受状态，要么都不处于接受状态。事实上，我们以状态对作为顶点构造一个有向图，满足从 [a,b] 指向 [c,d] 的边存在当且仅当 a,b 不等价可以直接推出 c,d 不等价，再由于接受状态和非接受状态是不等价的，通过在图中搜索，我们可以得到所有的等价状态对。

当我们得到等价状态对之后就自然地得到了等价状态类。用等价状态类来代替原来的状态之后，便可以得到与确定型的有限状态机等价的状态最少的确定型的有限状态机。这样得到的有限状态机是状态最少的，不然的话，考虑两个确定型的有限状态机之间的有限状态，就可以得到有两个等价状态类是等价的，这显然是矛盾的。

如果我们考虑不同有限状态机间的等价状态，我们便可以根据两个有限状态机的初始状态判断两个有限状态机是否等价。

结尾

以上就是有限自动机以及正则表达式相关的笔记。能读下来真是太感谢了……

下一个笔记会是上下文无关语言和下推自动机相关的内容，有兴趣的话欢迎来看。